In a trial of a new drug to cure cancer, 44 percent of 50 patients achieved remission after treatment. Without the drug, only 32 percent of previous patients did the same. The new treatment sounds promising, but is it better than the standard?
That question is difficult, so statisticians tend to answer a different question. They look at their results and compute something called a p-value. If the p-value is less than 0.05, the results are “statistically significant” – in other words, unlikely to be caused by just random chance.
The problem is, many statistically significant results aren’t replicating. A treatment that shows promise in one trial doesn’t show any benefit at all when given to the next group of patients. This problem has become so severe that one psychology journal actually banned p-values altogether.
My colleagues and I have studied this problem, and we think we know what’s causing it. The bar for claiming statistical significance is simply too low.
Most hypotheses are false
The Open Science Collaboration, a nonprofit organization focused on scientific research, tried to replicate 100 published psychology experiments. While 97 of the initial experiments reported statistically significant findings, only 36 of the replicated studies did.
Several graduate students and I used these data to estimate the probability that a randomly chosen psychology experiment tested a real effect. We found that only about 7 percent did. In a similar study, economist Anna Dreber and colleagues estimated that only 9 percent of experiments would replicate.
Both analyses suggest that only about one in 13 new experimental treatments in psychology – and probably many other social sciences – will turn out to be a success.
This has important implications when interpreting p-values, particularly when they’re close to 0.05.
The Bayes factor
P-values close to 0.05 are more likely to be due to random chance than most people realize.
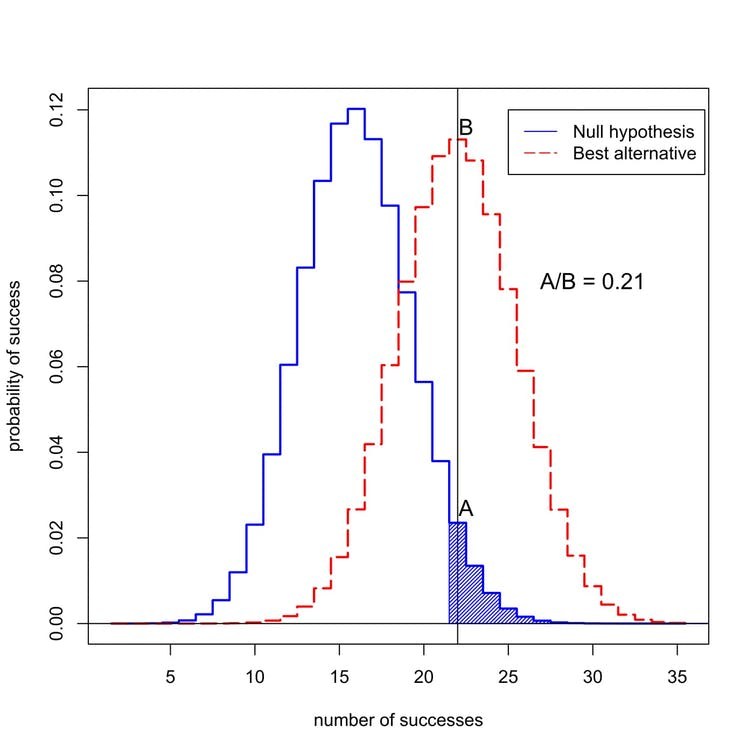
To understand the problem, let’s return to our imaginary drug trial. Remember, 22 out of 50 patients on the new drug went into remission, compared to an average of just 16 out of 50 patients on the old treatment.
The probability of seeing 22 or more successes out of 50 is 0.05 if the new drug is no better than the old. That means the p-value for this experiment is statistically significant. But we want to know whether the new treatment is really an improvement, or if it’s no better than the old way of doing things.
To find out, we need to combine the information contained in the data with the information available before the experiment was conducted, or the “prior odds.” The prior odds reflect factors that are not directly measured in the study. For instance, they might account for the fact that in 10 other trials of similar drugs, none proved to be successful.
If the new drug isn’t any better than the old drug, then statistics tells us that the probability of seeing exactly 22 out of 50 successes in this trial is 0.0235 – relatively low.
What if the new drug actually is better? We don’t actually know the success rate of the new drug, but a good guess is that it’s close to the observed success rate, 22 out of 50. If we assume that, then the probability of observing exactly 22 out of 50 successes is 0.113 – about five times more likely. (Not nearly 20 times more likely, though, as you might guess if you knew the p-value from the experiment was 0.05.)
This ratio of the probabilities is called the Bayes factor. We can use Bayes theorem to combine the Bayes factor with the prior odds to compute the probability that the new treatment is better.
For the sake of argument, let’s suppose that only 1 in 13 experimental cancer treatments will turn out to be a success. That’s close to the value we estimated for the psychology experiments.
When we combine these prior odds with the Bayes factor, it turns out that the probability the new treatment is no better than the old is at least 0.71. But the statistically significant p-value of 0.05 suggests exactly the opposite!
A new approach
This inconsistency is typical of many scientific studies. It’s particularly common for p-values around 0.05. This explains why such a high proportion of statistically significant results do not replicate.
So how should we evaluate initial claims of a scientific discovery? In September, my colleagues and I proposed a new idea: Only P-values less than 0.005 should be considered statistically significant. P-values between 0.005 and 0.05 should merely be called suggestive.
In our proposal, statistically significant results are more likely to replicate, even after accounting for the small prior odds that typically pertain to studies in the social, biological and medical sciences.
What’s more, we think that statistical significance should not serve as a bright-line threshold for publication. Statistically suggestive results – or even results that are largely inconclusive – might also be published, based on whether or not they reported important preliminary evidence regarding the possibility that a new theory might be true.
On Oct. 11, we presented this idea to a group of statisticians at the ASA Symposium on Statistical Inference in Bethesda, Maryland. Our goal in changing the definition of statistical significance is to restore the intended meaning of this term: that data have provided substantial support for a scientific discovery or treatment effect.
Criticisms of our idea
Not everyone agrees with our proposal, including another group of scientists led by psychologist Daniel Lakens.
They argue that the definition of Bayes factors is too subjective, and that researchers can make other assumptions that might change their conclusions. In the clinical trial, for example, Lakens might argue that researchers could report the three-month rather than six-month remission rate, if it provided stronger evidence in favor of the new drug.
Lakens and his group also feel that the estimate that only about one in 13 experiments will replicate is too low. They point out that this estimate does not include effects like p-hacking, a term for when researchers repeatedly analyze their data until they find a strong p-value.
Instead of raising the bar for statistical significance, the Lakens group thinks that researchers should set and justify their own level of statistical significance before they conduct their experiments.
I disagree with many of the Lakens group’s claims – and, from a purely practical perspective, I feel that their proposal is a nonstarter. Most scientific journals don’t provide a mechanism for researchers to record and justify their choice of p-values before they conduct experiments. More importantly, allowing researchers to set their own evidence thresholds doesn’t seem like a good way to improve the reproducibility of scientific research.
Lakens’s proposal would only work if journal editors and funding agencies agreed in advance to publish reports of experiments that haven’t been conducted based on criteria that scientists themselves have imposed. I think this is unlikely to happen anytime in the near future.
 Until it does, I recommend that you not trust claims from scientific studies based on p-values near 0.05. Insist on a higher standard.
Until it does, I recommend that you not trust claims from scientific studies based on p-values near 0.05. Insist on a higher standard.
###
By Valen E. Johnson, University Distinguished Professor and Department Head of Statistics, Texas A&M University
This article was originally published on The Conversation. Read the original article.